13.1 THE LINK BETWEEN DIMENSIONS, GEOMETRY AND VIBRATION
By now we should be more than ready to have a full disclosure about the meaning and importance of Platonic Solid geometry in understanding the multi-dimensional properties of “consciousness units,” as we have seen on the Earth.
To recap, our term “consciousness unit” (CU) refers to an area where the energetic, conscious “aether” or zero-point energy bleeds through into our physical space and time, taking up the form of a luminous sphere of electromagnetic energy that has a hole through the middle, which forms a north-south rotational axis.
From the last two chapters, we now know that these spherical energy formations are seen to have geometric vortexes within them as well. This information comes from scientific investigations of planetary behaviors as well as a straightforward mathematical analysis of the “tetrahedral” angles and ratios between the various objects located in the Cydonia area of Mars, which appear to be artificially created.
Straight-lined formations like these are usually thought to be manmade objects only, certainly not a part of nature, and thus for most of us the information in this chapter will be very unique. We have never tried to insinuate that any of the planets have gigantic, physical crystals in them, only that this is a shape that is formed by energy as it flows through the CU, which in turn forms the planet.
We are not accustomed to thinking of sound or color as having hidden geometric shapes in their vibration, and yet this is exactly what our research has now led us to conclude.
13.1.1 INTERDIMENSIONAL VORTEXES
In the last two chapters we have seen how all the planets show signs of having energetic upwellings at certain geometric points that are defined by shapes such as the icosahedron, dodecahedron and tetrahedron.
Energy streams in and out of the poles, with what seem to be two counter-rotating fields that join together to form these geometric patterns on the planet’s surface. (We will cover the how and why of this joining action in later chapters.) Luminous core material similar to the Sun is likely to exist inside the planets, and the problems with the dynamo model actively call for a better solution.
Returning to our discussion of the geometric areas themselves, on Earth we have seen that these areas can also have a powerful effect on the “vibrational” state of physical matter as well as the conditions of space and time. In short, it seems that:
These geometric nodal areas are somehow “interdimensional” vortexes of energy.
We have already speculated that this is because “higher dimensions” are simply areas that are all around us, where the aetheric energy is vibrating at a higher frequency than it is in our own level of focus. Now that we have seen the geometry of the tetrahedron, icosahedron and others throughout the entire Solar System, we should expect that all the planets are creating these gravitational and inter-dimensional vortexes of space and time in the same fashion.
Interestingly, in the Law of One series from the alleged extraterrestrial group known as Ra in 1981, very specific information is given about the understanding of vibration as being the key “missing link” in understanding higher dimensions.
They do not like to use the word “dimensions” but instead refer to them as “densities,” meaning that they are different densities of the One Unified Aetheric Energy Source that we have already written of in this book. The first quote relates the densities to vibrations of sound, and the second to vibrations of color:
RA: The term density is a, what you call, mathematical one. The closest analogy is that of music, whereby after seven notes on your western type of scale, if you will, the eighth note begins a new octave.
RA: The nature of vibration is such that it may be seen as having mathematically straight or narrow steps. These steps may be seen as having boundaries. Within each boundary there are infinite gradations of vibration or color.
However, as one approaches a boundary, an effort must be made to cross that boundary. These colors are a simplistic way of expressing the boundary divisions of your density. (B2, 42)
In the next quotations from Ra, we can see that they are aware of the geometric energies that we have observed on the planet as well, in keeping with the idea of higher dimensions being related to a fluidlike vibration:
RA: Imagine, if you will, the many force fields of the Earth in their geometrically precise web. Energies stream into the Earth planes, as you would call them, from magnetically determined points. (B1, 81-82)
RA: Love creating light, becoming love/light, streams into the planetary sphere according to the electromagnetic web of points or nexi of entrance. These streamings are then available to the individual who, like the planet, is a web of electromagnetic energy fields with points or nexi of entrance. (B1, 144)
Quotations from the Jane Roberts book Seth Speaks, from sessions conducted in 1968, clearly point to the tips of geometric objects as interdimensional “streaming points” as well, and go into further detail than Ra in certain respects:
…Other kinds of consciousness coexist within the same “space” that your world inhabits… You do not perceive them, and generally speaking they do not perceive you. This is a general statement, however, for various points of your realities can and do coincide, so to speak.
These points are not recognized as such, but they are points of what you could call double reality, containing great energy potential; coordinate points, indeed, where realities merge. There are main coordinate points, pure mathematically, sources of fantastic energy, and subordinate coordinate points, vast in number.
[Note: These “mathematically pure” points that Seth refers to are actually the tips of the Platonic geometries that we have been discussing. And the merging of realities is clearly seen in the Bermuda Triangle. Also, Seth could be speaking about the fact that two different fields are merging at these points to create their vortex qualities, hence the use of the word “double.”]
(Long pause at 9:29.) There are four absolute coordinate points that intersect all realities.
[Note: The only Platonic Solid that has four points is a tetrahedron. Seth’s quote here suggests that the tetrahedron is somehow “more important” than the other geometries, as Hoagland also believes from the Message of Cydonia, and later we’ll see why this is so.]
These [geometric] coordinate points [in general] also act as channels through which energy flows, and as warps or invisible paths from one reality to another. They also act as transformers, and provide much of the generating energy that makes creation continuous in your terms. (Many pauses.)
[Note: As the work of Richard C. Hoagland and The Enterprise Mission has shown, the points of the tetrahedron are indeed the source of tremendous energy upwellings in planets, such as the Great Red Spot on Jupiter.
And again, the points of the icosahedron on Earth are clearly demonstrating warps from one reality to another. As a general rule, when there are many pauses in Jane’s speech patterns as Seth, it means that she is in an extremely deep level of trance to bring forth the information.]
Your space is filled with these subordinate points, and as you will see later, these are important in allowing you to transform thoughts and emotions into physical matter. When a thought or emotion attains a certain intensity, it automatically attracts the power of one of these subordinate points, and is therefore highly charged, and in one way magnified, though not in size.
These points impinge upon what you call time, as well as space. There are certain points in time and space, therefore, (again in your terms), that are more conducive than others, where both ideas and matter will be more highly charged. Practically speaking, this means that buildings will last longer; in your context, that ideas wedded to form will be relatively eternal. The pyramids, for example, are a case in point.
[Note: This may seem confusing now, but later we will see how these geometries do affect time as Seth is suggesting here. Seth’s quote about matter being stronger at these points is in keeping with our observations that matter is far more flexible than we have ever believed.
Under different circumstances such as those of a tornado, matter can change phase to become weaker, and now Seth is telling us that the same forces, in a less chaotic form, can strengthen it as well.]
(Slow at 9:43.) These coordinate points – absolute, main, or subordinate – represent accumulations or traces of pure energy, minute to an extreme if you are thinking in terms of size – smaller than any particle of which your scientists know for example, but composed of pure energy. And yet this energy must be activated. It is dormant until then – and it cannot be activated physically.
[Note: This is exactly what we will find out at the beginning of Part Two – at the smallest subatomic level, geometry is the hidden key to the “pure energy” of the aether.]
(9:50.) Now: A few clues here that might help you, or mathematicians. There is an ever-so-minute alteration of gravity forces in the neighborhood of all of these points, even of the subordinate ones, and all the so-called physical laws to some extent or another will be found to have a wavering effect in these neighborhoods.
The subordinate points also serve in a way as supports, as structural intensifications within the unseen fabric of energy that forms all realities and manifestations. While they are traces or accumulations of pure energy, there is a great difference between the amount of energy available in the various subordinate points, and between the main and absolute points… (session 524)
[Note: This prediction bore itself out in the observations of the Oregon Vortex, which is obviously one such area of energetic charge. Gravity did make a noticeable change within the vortex, as well, as the passage of time and the sizes of physical objects.]
Therefore, in the areas such as Sanderson’s twelve vortices of the icosahedron on the Earth, the extraterrestrially-derived information tells us that these bizarre effects are showing us cases where the fluidlike, vibrating aether is bleeding through to our reality at a higher level of density than the energy that is normally around us.
And if that energy is at a higher “density,” then it would transform all matter in its vicinity, including human life, into a higher density as well. And here we have a very convenient, new explanation for the phenomena that we have already been investigating.
Ra’s idea of “higher dimensions” being part of an Octave of densities actually makes very good sense and answers many current paradoxes of science. Then, all we have to do is see that there is one single “aether” throughout the universe, and it follows the basic patterns of music and vibration to differentiate itself. This completely explains many long-standing mysteries, as we will again explore in the next chapter. Seth makes this point as well:
Now anything that appears in physical terms also exists in other terms that you do not perceive. You only perceive realities when they achieve a certain “pitch,” when they seem to coalesce into matter. But they actually exist, and quite validly at other levels… (session 530)
[Note: Notice the use of the word “pitch.” It is not at all a simple metaphor, but a very accurate statement of the Harmonic Universe and its function with aetheric energy densities.]
Yours is not a system of reality formed by the most intense concentration of energy, therefore. It is simply the one you are tuned into, part and parcel of. You perceive it simply for this reason.
Other portions of yourself, therefore, of which you are not consciously aware, do inhabit what you would call a supersystem of reality in which consciousness learns to handle and perceive much stronger concentrations of energy, and to construct “forms” of a different nature indeed… (session 530)
And another quote:
You understand that there are spectrums of light. So are there spectrums of matter. Your system of physical reality is not dense in comparison with some others. The [three basic] dimensions that you give to physical matter barely begin to hint at the varieties of dimensions [that are] possible… (session 567)
So here, we again have the analogy of “spectrums” of dimensions – in other words, existing within an Octave structure. Matter itself, being formed of aether, must also be subject to its changing vibrational levels, and thus potentially be able to move from one reality to another.
This could explain how tornadoes are able to fuse solid objects together, and why disappearances occur in the icosahedral vortices on Earth. Furthermore, Seth and Ra both insist that our consciousness is the key link that connects us with these other levels of reality; we are, in fact, multi-dimensional beings who have lost our awareness of the “big picture.”
Bearing that in mind, an investigation of the properties of light, sound and geometric vibrations and how they work together is very well suited to our discussion at this point. This will be general material, but it is vital for us to have it in this form before we proceed into the next chapter of discussion on the dimensions. Both Seth and Ra suggest that we need to explore these interconnecting properties of vibration more closely in order to find our deepest answers.
13.2 SOUND
The easiest and most familiar way to study vibration is through sound. Any musician will tell you that all vibrations of sound are grouped into octaves, and we know that “oct” means the number eight. In an octave there are seven fundamental “nodes” of vibration followed by an eighth. The eighth note has two purposes, in that it not only completes one octave but it also begins the next.
Greek mathematician and philosopher Pythagoras, through a straightforward process of repeatedly dividing a frequency by five, is credited as being the first to devise these eight “pure” tones of the octave, known as the Diatonic scale. He started by taking a single-stringed “monochord” instrument and measured its exact lengths when different notes were played.

Then, just like playing a guitar, he pressed his finger down on different lengths of the string and strummed it to get different notes. Each note that he played would divide the string into two different sections, and the relative lengths of the two sections would then be measured and written down for each note.
Pythagoras then showed that the frequency (or vibrating speed) of each note could be represented as a ratio between the two string lengths, or two numbers – hence the term “Diatonic ratios.” Further research in dividing by fives led him to construct the Octave as the simplest grouping of the various ratios involved, such as 1:1, 2:1, 3:2, 5:3, 13:8 and 21:13.
We can see the Diatonic scale on a piano as the white keys, providing that the beginning note in our octave is a C. The piano has black keys as well, and when they are included, there are a total of thirteen notes in the Octave, with the thirteenth note also being the first note in the next octave.
These thirteen notes are known as the Chromatic scale, and most of the world’s music will consist only of notes that fit somewhere within this scale; therefore almost all possible songs can be played on a piano. (As one exception, Indian music will use notes that do not fit in a chromatic scale, called quartertones or microtones.)
Mathematics aside, the most basic reason why the number eight was chosen instead of thirteen for the “octave” grouping of musical notes is that all eight “diatonic” notes will sound pleasant together; in other words, they will be harmonic.
You can play a song on the white keys of the piano and it will always sound like music, regardless of what notes you play. However, if you experiment with the chromatic scale without knowing what you are doing, painful dissonance is most likely soon to follow and anyone else in the room will quickly ask you to stop.

Mathematically, the highest note in an Octave has a vibration speed or frequency that is twice as fast as the lowest note, and that is the most basic way to see how an Octave organizes one full group of sound vibrations.
Every note, whether A, B, C, D, E, F or G, will be doubled in its value in the next octave.
Since the octaves are continually doubling in their vibration, there are only a handful of octaves within the range of human hearing. Above a certain point the vibrations will become too fast for human ears to detect, even though they will still exist all around us.

13.2.1 ALL POSSIBLE VIBRATIONS
So, just as the alphabet encompasses all possible words in our language, the octave structure encompasses all possible vibrations of sound, and reveals the simple way that they fit together. Chaos theory might call the Octave an “attractor,” meaning that all vibrations of sound, however “chaotic” or random they might be from one to the next, must be ‘attracted’ into the Octave structure.
What about other non-musical sounds like the wind, you ask? How could the sound of wind fit into an Octave of musical notes? “White Noise” is a technical term for high-speed, randomly scattered fluctuations of sound frequency that do not produce any apparent tone, but rather create a hissing noise like you would hear in the air escaping from a tire.
Although there may be thousands of overlapping frequencies in this noise, we know that once they are all properly isolated, every one must automatically be part of an Octave on some level. There are simply too many different tones occurring too quickly for our ears to discern one from another.
13.2.2 SOUND IS SIMPLY A VIBRATION OF AIR
From a scientific point of view, a sound is defined as nothing more than a vibration of molecules of air. Mathematically, we measure sounds in terms of how many times air vibrates in one second of time. This gives us a numerical value, and thus anyone who has ever played a stringed instrument knows that the average tuning fork will say “A 440.”
This means that the note that we call A is recognized as nothing more than 440 vibrations of air in one second of time. A different note would have a different number, and therefore 440 vibrations of air per second must always be an A. That’s all there is to it. And later, we will see that these “harmonic” number values are of tremendous importance in measuring and analyzing the behavior of the aether.
DIATONIC SCALE NUMERICAL FREQUENCIES:
| 288 | 324 | 360 | 384 | 432 | 480 | 540 | 576 |
| D | E | F | G | A | B | C | D |
(Note: “A” slightly adjusted- explained later)
Providing that you are not in a total vacuum, the density or composition of the air that is vibrating does not matter either, as a musical instrument will sound the same on top of Mount Everest, where the air is thinner, as it would at sea level where the air is much denser.
However, even the air itself is not necessary; all we need is something, anything, that vibrates. For example, we can hear these same sounds underwater, such as in the songs of the whales. The metal on a tuning fork, when struck, can create sound just by holding the base of the fork to your skull and allowing it to resonate through your body.
So the medium itself does not directly affect the tone or pitch of the sound; the vibrations can occur in clean air, dirty air, clean water, dirty water, metal, flesh, bone or other forms as well, including cloth fiber, as in the case of the old-fashioned “telephone” composed of two tin cans connected by a long string.
In that case, when the string is pulled tightly between the two cans and one person talks into their can while the other listens, the string will also carry the sound vibrations along in the same fashion, though they will be distorted. In short, the vibrations of sound do not just occur in air – they fundamentally vibrate through everything. Hearing sound is simply a way for us to directly perceive and experience vibrations.
Even though we are accustomed to thinking of these fundamental sound vibrations as only having meaning and importance to our ears, this book has already started showing us that these simple vibrations of the Octave underlie all of reality as we know it. The unseen ‘incompressible fluid’ of the aether, or the “spiritual energy” that forms the Ultimate Being of our universe, can be unequivocally shown to vibrate according to these principles, as we have already seen on the planets.
And thus, just as the Hindus had proposed the idea that the AUM is the primal sound that formed the Creation, we can now see that sound constructs the Universe, and music is a way for us to physically hear and experience the essence of God itself. We ourselves are ultimately composed of living, dancing musical waveforms; God’s creation.
Without music in our lives, we deny ourselves the very inner knowledge and enjoyment of our own existence.
13.3 LIGHT
An identical level of this octave of vibration occurs in the visible light spectrum, where we have white light that can be broken down in a prism or rainbow into seven colors – red, orange, yellow, green, blue, indigo and violet – before starting a higher level or octave of vibrations, such as infrared and ultra-violet.
And we now know that the frequency of visible light, as a rippling “disturbance” of fluidlike aetheric energy, is simply on a higher octave of vibration than the frequencies of sound in the musical octave.
To put it more simply, you could take the numerical ratios between each note in the musical Diatonic scale and double them many times over, and eventually you would find the same, identical ratios between the vibrational speeds of the light spectrum. The only difference between them is the magnitude; sound is vibrating much more slowly, whereas light is vibrating much more quickly.
| OCTAVE | FREQUENCY | NOTE | COLOR |
| 48 | 316659348799488 | D | |
| 56241767399424 | E | ||
| 375299968947541 | F | INFRA-RED | |
| 422212465065984 | G | RED | |
| 474989023199232 | A | ORANGE-YELLOW | |
| 534362651099136 | B | YELLOW-GREEN | |
| 562949953421312 | C | GREEN | |
| 49 | 633318697598976 | D | GREEN-BLUE |
| 712483534798848 | E | BLUE-VIOLET | |
| 750599937895082 | F | VIOLET | |
| 844424930131968 | G | ULTRAVIOLET | |
| 949978046398464 | A |
From Dale Pond’s Physics of Love: “The above relationships are derived by computing Pythagorean frequencies and intervals beginning in the audio range of sound.
Although there are many shades of, say, Green ranging from above B to below D there is really only one C at 512 cps in the lower audio octave. These colors pertain to pigments and not to hues of light which would be C=Red, D=Orange, E=Yellow, F=Green, G=Blue, A=Indigo and B=Violet.”
13.3.1 LIGHT SPEED
When any of the light frequencies or wavelengths travel through space, they move at what most believe to be a constant speed, cited as roughly 186,000 miles per second. However, this observation does not see light as conducting through the aetheric medium at a given speed.
Most think that nothing in the universe can exceed this rate, so the speed of light or “c” is the fastest movement or vibration that we normally recognize from our perspective here on Earth in the third dimension. New sources suggest that “c” is only the fastest vibration under natural conditions in the third dimension.
As published in The New York Times in May of 2000, abnormal conditions in the laboratory, such as a tube with cesium gas under high pressure that is illuminated by light coming in “sideways”, can create light speeds up to three hundred times faster than “c”. This is identical in form to Bearden’s “scalar wave interferometry” experiments.
So if we were to group all possible vibrations together in a chart, we would have a complete lack of motion on the bottom of our graph, and the speed of light on the top. In this way, light speed defines the edge or the boundary of vibrations in our reality.
Unlike what Einstein suggested, moving an object to light speed may not create infinite density in matter; instead sources such as Ra would categorize light speed as the peak of vibrations in the third density, or dimension.
If we move into an area or “domain” where aether moves at a higher speed, then light speed changes and matter naturally “focuses” into this new vibrational level. This conforms with observations of tornado anomalies and vortex anomalies alike, which show space, time and matter changes.
The very first words of the book of Genesis in the Bible are, “In the beginning, God said, ‘Let there be light,’ and there was light.” Ultimately, we can demonstrate that all vibrations that create our universe are simply different forms of this one unified conscious energy.
Without wearing and seeing the bright reds, blues, greens, yellows, purples and oranges of Light around us in daily life, we deny ourselves the very inner knowledge and enjoyment of our own existence. A life without color is indeed “dull” and “gray,” “gloomy” and “black.”
13.4 GEOMETRY
Geometry completes the basic triad of our perception of the fundamental building blocks of vibration in the Universe – that triad being light, sound and geometry. With the geometries that we have already been discussing, the sounds of music and the colors of the rainbow suddenly spring into physical form.
Suddenly, the abstract concepts of harmony and color reveal structures composed of straight and curving lines that we can then make models with and build things out of. Although we can see color and hear sound, we do not normally think of a physical geometric shape in two or three dimensions that would precisely represent these vibrations.
However, numerous researchers such as Gerald Hawkins, Buckminster Fuller and Hans Jenny have shown that sound vibrations will form specific geometric patterns, providing that what you are vibrating is visible instead of air, which is normally not visible.
Gerald Hawkins did not actually arrive at his findings through studying vibration. In his case, he was led to make his discoveries after spending years investigating the “crop circle” phenomenon, where complex geometric patterns would show up overnight in various grain crops around the world, usually visible only from the air.
After studying hundreds of these formations, Hawkins realized that certain patterns were repeating themselves, and the underlying unity among these patterns was expressed by taking simple two-dimensional geometric shapes such as a triangle, square and hexagon and fitting them precisely inside of a circle, so that all tips of the shape perfectly touched the circle’s edge.
To his amazement, the surface area of the inner geometries, when divided against the area of their outer circles, showed the exact same relationships responsible for the vibrations of music in the Octave – the “diatonic ratios” that we mentioned above. This is exactly what Pythagoras demonstrated with his one-stringed “monochord” instrument, only now instead of a ratio of string lengths, we have a ratio of geometry that indicates the same thing.
He realized that this was a totally new and unrecognized set of theorems in geometry, and not a single academic authority who he consulted with was familiar with these concepts. So in two dimensions, we can understand sound as being a “flat” geometric vibration, such as a triangle, that emerges within a “flat” circle.

13.4.1 FULLER’S BALLOON
Although Hawkins’ work came about in the 1980s and only covered two dimensions, decades-earlier experiments by students of Dr. Buckminster Fuller were the first to prove that sound vibrations are innately three-dimensional in their structure. Fuller’s students later used a spherical white balloon in order to achieve this effect, dipping it in a bath of dark-colored dye and vibrating it with pure Diatonic sound frequencies.
As expected, the dye would only be able to collect and stain on those areas of the balloon that were experiencing the least amount of movement. These areas were evenly spaced “nodes” or points where all of the violent motions on the surface of the balloon canceled themselves out to a “null zone” where the dye could easily accumulate.
Furthermore, faint and perfectly straight lines of dye could be seen connecting these nodes together. In this manner, sounds became directly visible as simple three-dimensional geometric shapes that formed crisscrossing straight lines over the balloon itself.
 |
 |
 |
 |
 |
| Octahedron | Star Tetrahedron | Cube | Dodecahedron | Isocahedron |
The “Platonic” Solids were revealed as sound vibrations in experiments inspired by Buckminster Fuller.
When looking at these shapes, we remember that they all fit perfectly within a sphere and that their tips are the “nodes” that were first detected. It is also important to remember that the sphere itself is the most harmonic shape of all, forming the foundation for all the other geometries within itself.
13.4.2 CYMATICS
Dr. Hans Jenny was captivated by the findings of Fuller and his students that vibrations were three-dimensional, and he sought to prove it in ways that were simpler and less cumbersome than using a balloon dipped in dye.
In Dr. Jenny’s scientific study known as “Cymatics,” he showed the geometry of sound vibrations using thin containers filled with media such as sand, Lygodium mold spores, wet plaster and various forms of liquid that had extremely tiny but visible particles or “colloids” floating in them. The experiments with colloidal liquid are of the greatest interest to us in this book.
At rest, the colloids would be evenly distributed throughout the liquid, which would then appear to resemble cloudy water. Dr. Jenny refers to this state as “hydro-dynamic dispersion.” When the container was vibrated with pure, Diatonic sound tones, however, the particles in the liquid would gather into orderly and discrete visible geometric patterns – many of which could be seen as both two and three-dimensional in their structure.
In other words, one could look at the images that were formed and clearly perceive depth within them – they were not simply “flat.” This is one of the most important things to study and remember in our entire book so far, as it provides an irrefutable, visual proof of the concepts that we have discussed.

Example of Hans Jenny’s Sound Vibrations in Colloidal Water Mixture
As pictured before, there are only five basic three-dimensional shapes to consider, and we know them as the Platonic Solids, since Greek philosopher Plato is credited with devising them. It is important to be very clear that when we look at these shapes, we are literally seeing vibration. The shapes themselves may not “exist” like a physical object, as like a hologram, if you tried to grab them or disturb them they would simply disappear, the vibrations then rippling around your fingers.
Nevertheless, while undisturbed, the shapes do have an existence as a vibration that is very real – and that existence can also create pressure, similar to the push that you feel on your body from a very loud sound or clap of thunder.
Now that we have seen these shape vibrations operating in the fluid-like aether, we know that their pressure-inducing force lines give us a dramatic new view of the dynamics of gravity.
With the redundant, obvious ways that these geometries mold the surface structural features of the Earth, such as continents, undersea ridges and mountain ranges, we can never be blinded to the truth again. It is only a matter of time before this simple observation will become common knowledge within the mainstream of humanity.
It is also very important to mention that when Fuller’s students increased the frequency in the balloon or Jenny increased the frequency in the water, the older forms would dissolve and disappear, and a more highly complex geometric form would take its place. This also could work in reverse, as when the frequency was turned back down to its original point, the original geometry would re-emerge in precisely the same shape.
So therefore, when studying the dynamics of the aether we will see that when you increase the vibrational frequency (or stress) of energy in a local area, the geometry itself in that local area, such as that which molds the Earth, will spontaneously transform into a higher order of complexity. And this raising and lowering frequency effect occurs all throughout the Creation – including the bodies within our own solar system as it moves through the Galaxy.
Dr. Spilhaus’ work has shown us that our own gravitational field here on Earth has already been through several such transformations since the time of the original “mega-continent” Pangaea, which actually represents the time when Earth had a uniform crust – prior to the enlarging movement now seen in the science of Global Expansion Tectonics, which began well back in 1933 with Otto Hilgenberg.
13.5 SPIRALS
And so, the simple geometric patterns formed by sound vibrations (and therefore light vibrations on a higher magnitude as well) can be seen in both two and three dimensions, and the two-dimensional forms such as the triangle, square and hexagon discussed by Hawkins are probably more familiar to us than the three-dimensional forms revealed by Fuller and Jenny, though we have now seen these geometries at work in the planets.
Very importantly, these vibrational geometries can also grow and contract in size, and simple, visible geometric structures organize and control these movements as well. When we start fitting these shapes inside of each other, they indeed form a “nested” appearance, with each successive shape growing harmonically larger than the one before it.
We will show more of this as we go along. This “sphere within sphere” geometry has already been seen in various experiments, and now we can expect the various geometric harmonies to exist inside these expanding spheres as well.
The simplest way to model the geometric expansion from one shape to another is by tracing out how the nodes move relative to each other. We remember that on Earth, the expanding geometric movements have been called “radial” or “spiraling” by Spilhaus and others.
The simplest way to chart the movement from node to node between two different shapes would be with a spiraling line, which Ra calls “the spiraling line of light.” These spirals include the Fibonacci or “Golden Mean: as well as the spirals created by the square roots of two, three and five. We will now show that these spirals are directly related to musical frequencies through mathematics.
13.5.1 THE PHI SPIRAL
Fundamental to all studies of spirals is the most important of them all, known as the Golden Mean, Fibonacci or “phi” spiral. To best understand this spiral, we start with the innately harmonic, vibrational way that it is created through number summing. Essentially, we will see that each new number is the sum of the previous two.
Typically we start with one and add it to itself. That gives us a product of two. Then we take two and add it to the number before it, which was one, and that gives us three. Then we take three and add it to the number before it, which was two, and we get five. And on it goes as follows:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…
So, the numbers continue to expand in a simple, harmonic way, where each new number represents the sum of the two numbers that came before it. If we divide the above pairs of numbers into each other, in the earlier stages we will see all the common Diatonic musical ratios that Pythagoras discovered such as 3/2, 5/3, 8/5, 13/8 and 21/13.
This should not surprise us, as music is a vibrational motion, and the summing technique used in phi is a form of vibration as well. The elegant nature of this vibration is easily seen in drawings of the “phi spiral,” pictured below.
To better understand how this spiral works with the Platonic Solids, it should be viewed as a three-dimensional object, as though it were wrapped around a cone with the top point at G and the bottom point at A. This type of three-dimensional spiral shape is called a “conical helix.”

Fibonacci or “phi” spiral and geometric counterparts.
Although the early stages of the “phi” number series will form the musical ratios between themselves, as the number pairs get higher and higher, the ratios between them become more and more similar, and the growth process stabilizes.
Ultimately, as you go higher every pair of numbers in the series will divide together to form the exact same number, meaning that the ratio between all the numbers remains constant. For this reason, the ratio is called a “constant” as it will always be the same, and the number, (which continues endlessly,) is:
1.618033988749894848820…
Another interesting fact is that we can start with any two numbers, regardless of their difference, and begin summing them using the simple formula above. No matter how different they might be, within a short period of time we will again create the constant “phi” ratio between the two of them.
This entire concept has inspired countless generations of mathematicians, musicians, scientists and philosophers, as it mysteriously shows up in many different guises, including the growth proportions of plants, animals and human beings. As we have said, the musical ratios of “phi” provide the structure for simple geometry in both two and three dimensions, which we now know is another form of vibration.
The above diagram demonstrates this, as we can see that there are actually six isosceles triangles of identical proportions represented as the spiral continues to expand. The size ratio between each of the triangles will be the “phi” constant of 1.618…, given above.
These spirals can show us how simple geometric forms such as the square or triangle can grow larger and larger or smaller and smaller. As the spiral either unfolds or infolds, so too will the geometric shapes that can be formed within it either expand or contract. (In other words, if the above spiral were radiating outward, then the triangles would get progressively larger. If the spiral were compressing inward towards point F, then the triangles would get progressively smaller.)
It is this very principle of the spiral that allows the simple, expanding growth patterns of Nature to formulate themselves, both in crystal structures as well as living organisms. If we were to map out the geometry of how the simpler geometries on Fuller’s spherical balloon expanded into their more complex forms when he raised the vibration, we would see that their expansions could be precisely mapped with the simple, harmonic spirals mentioned above.

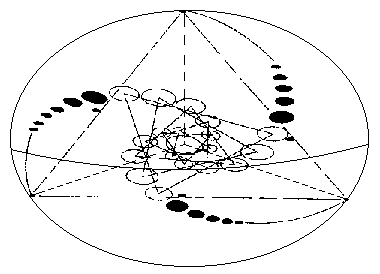
Spherical, ratcheting expansion of tetrahedral shape along fractal-based spiral pathways.
The above diagram is derived from a huge and extremely dramatic crop formation named the “Triple Julia Set” that appeared overnight in a grain field in England in 1996. It is a model of how this system of interconnecting spirals and Platonic geometry looks when expanded into three dimensions.
The original crop formation only consisted of the three spirals made up of individual circles, and all straight lines as well as the outer sphere and equator have been added in to better illustrate what we are seeing here. Ultimately, it is a model for the vibration of the aether that is creating visible planetary energy stresses as well as perfectly measurable structures in time.
For now, we should also visualize each triangle as being a tetrahedron that has its own spherical field, thus making this a geometric diagram of the “mastrioshka” or “nested doll” spheres of energy that we have seen in many experiments such as those done by Dr. Chernobrov.
13.6 FORM AND GROWTH, SPACE AND TIME, MALE AND FEMALE
And so, we can already see why the Ancients referred to straight and curved lines as the two apparent opposites in the Universe, even though they are actually unified as vibration. Ultimately we feel that in one way of thinking, the straight lines and geometries can represent space, and the curved lines and spirals can represent time.
But for now we will put it in more familiar terms and say that straight lines create form, and curved lines create the movement and growth of that form. In other words, straight lines form the geometric structures of the vibrations themselves, and curved lines form the pathways for these structured frequencies to expand and contract.
Although we normally don’t think of curving geometry with sound and light, we know that these spirals govern the movement between one note in the octave and the next higher note, or one color in the spectrum and the next higher color.
To put all this in a more spiritual context, in many ancient mystical traditions the straight line was thought of as the masculine force, associated with the Sun, and the curved line was thought of as the feminine force, associated with the Moon. These masculine-feminine associations are quite easy to intuitively work out in our own minds.
At rest, the sperm cell forms a straight line, whereas the egg is a rounded structure. Men’s bodies are harder and more straight-lined in construction and women’s bodies are more smooth and curvaceous. Men’s minds tend to think in more linear, rigid, mathematical “left brain” patterns and women’s minds tend to think in more curving, fluid, emotional “right brain” patterns.
Primitive men hunted and built by the light of the Sun, using straight spears and arrows to catch prey – or more recently, straight boards, hammers and nails to build structures, whereas women cooked and served food in smooth, curved bowls of pottery or wood and nurtured their young with smooth, curved breasts in the secluded darkness of the cave, igloo, teepee or longhouse, nestled away from the light of day where predators and villains once roamed.
Furthermore, women are directly connected with the Moon in ways that men could never be, through their menstrual cycle, showing another level of why the Ancients associated the feminine spirit with our own Midnight Sun.
13.7 SACRED GEOMETRY AND LIFE
The study of these various geometric forms and spirals, including their spiritual connections to humankind as partially illustrated above, is known as “sacred geometry,” and Robert Lawlor’s book of the same title is arguably the best existing reference on the subject.
Many of history’s greatest scholars studied the principles of sacred geometry in extensive detail, as they were fascinated to discover that lifeforms of every possible variety on Earth demonstrated these musical, vibrational principles involving the interplay of space and time – straight and curving lines.
Simple seashells provided perfect representations of the Fibonacci spiral, as did the growth pattern of plants, the fingerprints, the horn of an ox, the interior of a sunflower or lotus and many, many different proportions in the skeletal structures of animals and human beings. There are obviously no limits to how far these principles will go, providing that someone is willing to mathematically study each plant or organism separately in search of these connections.
Since our current scientists give us no reason to believe that such harmonic principles are necessary in the growth of lifeforms, then why do they exist? If these proportions were not important, then why do we see them so repetitively?
Indeed, are we simply ignoring the evidence that is all around us – evidence that proves that everything in the Universe is a product of vibration? If the fundamental energy that constructs all of reality is vibrating in harmonic resonance, would it be possible for anything not to have a harmonic foundation?
13.8 SPIRAL RATIOS IN PLATONIC SOLIDS
Just so that we can conclusively demonstrate that spirals connect all the Platonic Solids together, we will pull a chart excerpt from The Shift of the Ages that makes our point. In Robert Lawlor’s quintessential book Sacred Geometry, we learn that the Hindus resolved the Platonic Solid geometries into an octave structure like we see for sound and light, and in the next table we have listed this geometry in order.
This gives us a complete, unified view of how the various vibrations work together, which we will see in the next chapter. For now, we should just be aware of what this graph represents. This is formed by assigning a length of “1” to the edges of the cube, and then comparing how larger or smaller the edges of the other forms are in relation to it.
We remember that in the Platonic Solids, every face is the same shape, every angle is identical, every node is evenly spaced from the others and every line is the same length.
|
1. |
Sphere | [no edges] |
| 2. | Central Icosahedron | 1 / phi2 |
| 3. | Octahedron | 1 / sq. rt. 2 |
| 4. | Star Tetrahedron | sq. rt. 2 |
| 5. | Cube | 1 |
| 6. | Dodecahedron | 1 / phi |
| 7. | Icosahedron | phi |
| 8. | Sphere | [no edges] |
Harmonic Proportions of Platonic Solids.
In the next chapter we will make a very compelling case that the ancient Hindus knew everything that we have discussed about these energy fields so far, and more. We were fortunate enough to locate a rare reprint of Rama Prasad’s 1894 book, Nature’s Finer Forces: The Science of Breath and the Philosophy of the Tattvas, from Kessinger Publishing.
We will see that the word “tattvas” has a similar meaning to our word “vibrations.” The amount of overlap between what we have seen up until this point and the data in Prasad’s book should be nothing short of dazzling, as almost every key aspect of the aetheric model that we have covered so far is contained in the pages of this book in one form or another.
We will also take a closer look at how the ancient aetheric concept of an “octave” of dimensions correlates with modern scientific studies, and show that there is a lot less difficulty in rectifying the two opinions together than we may have thought.
Furthermore, by understanding how geometry intersects with higher dimensions, as we have already seen on the planets, the idea of “hyperdimensional physics” moves out of the realm of theoretical speculation and into the arena of an applied science. And once we can apply these concepts, we open up a door to the Universe…




![DECLAS: Social Media Nukes An Entire Generation… But Why? [Free Ebook!]](https://divinecosmos.com/wp-content/uploads/2019/06/DECLAS_TT-150x150.jpg)